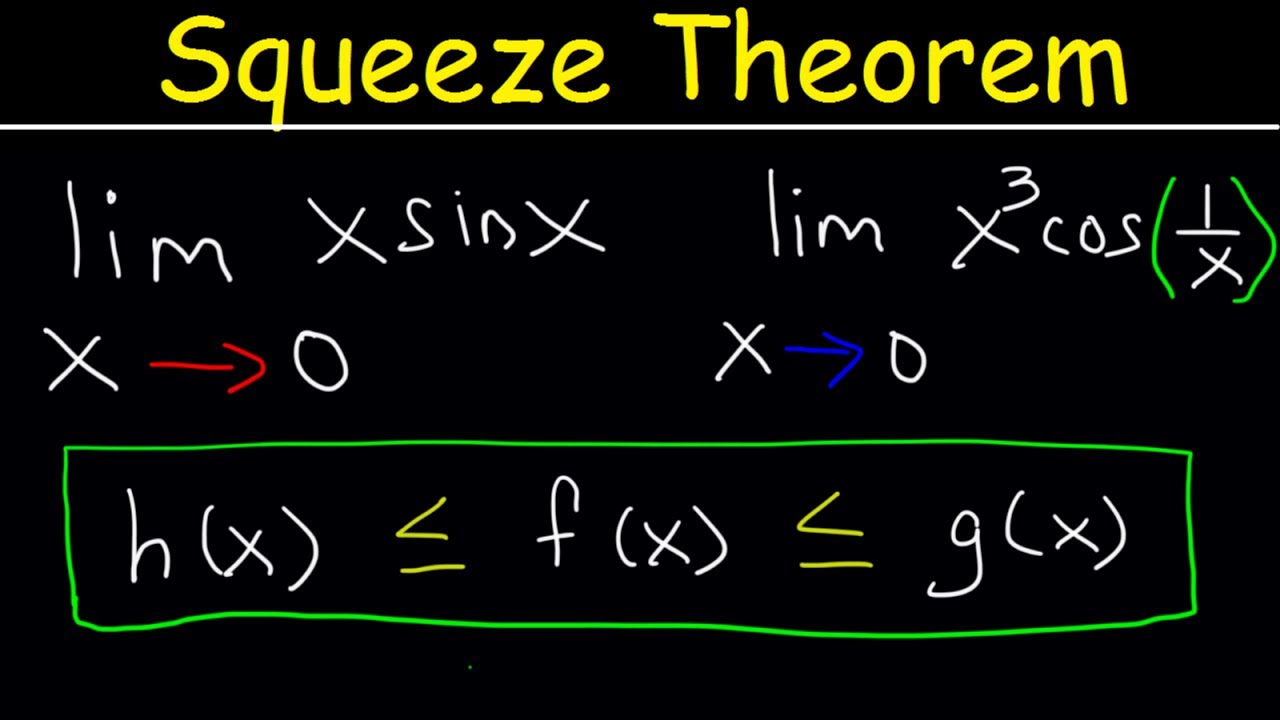Squeezing Success: Understanding The Squeeze Theorem In Calculus

Mathematics is a fascinating subject filled with intricate concepts and theorems that help us understand the world around us. Among these concepts, the Squeeze Theorem stands out as a powerful tool in calculus, enabling us to determine the limit of a function that is difficult to evaluate directly. This theorem is especially useful in cases where we can 'squeeze' a function between two other functions that have the same limit at a particular point. By exploring the Squeeze Theorem, we can uncover the beauty and elegance of mathematical reasoning.

The Squeeze Theorem, often taught in introductory calculus courses, provides a clear methodology for evaluating limits. It is particularly useful when dealing with functions that oscillate or behave erratically near a certain point. By establishing bounds for such functions, we can confidently assert the existence of a limit, even if the function itself defies simple evaluation methods. Through this article, we will delve into the details of the Squeeze Theorem, its applications, and examples that illustrate its usefulness in real-world scenarios.

As we embark on this mathematical journey, we will answer common questions surrounding the Squeeze Theorem, providing clarity and insight into its significance. Whether you are a student grappling with calculus concepts or simply someone intrigued by the wonders of mathematics, this exploration of the Squeeze Theorem will enhance your understanding and appreciation of this essential theorem.

What is the Squeeze Theorem?

The Squeeze Theorem, also known as the Sandwich Theorem, formalizes the idea of 'squeezing' a function between two other functions. In mathematical terms, if we have three functions, f(x), g(x), and h(x), such that:

• g(x) ≤ f(x) ≤ h(x) for all x in some interval around a point (except possibly at the point itself)
• lim (x → a) g(x) = lim (x → a) h(x) = L

Then, we can conclude that lim (x → a) f(x) = L. This theorem allows us to determine the limit of f(x) without directly computing it.

How Does the Squeeze Theorem Work?

The Squeeze Theorem operates by leveraging the behavior of functions around a specific point. By finding two bounding functions that converge to the same limit, we can infer the limit of the function in question. This method is especially effective for functions that exhibit oscillatory behavior, such as sine and cosine functions. The key steps in applying the Squeeze Theorem include:

1. Identifying the function f(x) whose limit we want to determine.
2. Finding two functions g(x) and h(x) that bound f(x) from below and above.
3. Proving that g(x) and h(x) have the same limit at the point of interest.
4. Concluding that f(x) must also converge to that limit.

What Are Some Real-World Applications of the Squeeze Theorem?

The Squeeze Theorem is not just an abstract mathematical concept; it has practical applications in various fields. Some notable applications include:

• Physics: In physics, the Squeeze Theorem can be used to analyze oscillating systems and determine the limits of certain physical quantities.
• Engineering: Engineers often apply the Squeeze Theorem in control systems to ensure stability and predict system behavior.
• Economics: Economists can utilize the Squeeze Theorem to model limits in economic functions and study market behaviors.

Can You Provide an Example of the Squeeze Theorem?

To illustrate the Squeeze Theorem in action, let's consider the example of the function f(x) = x² sin(1/x) as x approaches 0. This function can be challenging to evaluate directly, but we can apply the Squeeze Theorem:

First, we know that the sine function is bounded between -1 and 1:

• -1 ≤ sin(1/x) ≤ 1

Multiplying through by x² (which is non-negative for x near 0), we have:

• -x² ≤ x² sin(1/x) ≤ x²

Next, we take the limits of the bounding functions as x approaches 0:

• lim (x → 0) -x² = 0
• lim (x → 0) x² = 0

Since both bounding functions converge to 0, we can conclude by the Squeeze Theorem that:

lim (x → 0) x² sin(1/x) = 0.

What Are the Common Mistakes When Using the Squeeze Theorem?

While the Squeeze Theorem is a valuable tool, students often make mistakes when applying it. Here are some common pitfalls to avoid:

• Failing to verify the bounding functions: Ensure that the bounding functions truly enclose the function in question.
• Ignoring the conditions of the theorem: Remember that the limits of the bounding functions must be equal for the theorem to apply.
• Overlooking the interval of interest: The theorem applies only in a specific interval around the point of interest, so be mindful of this when selecting bounds.

How Can I Master the Squeeze Theorem?

Mastering the Squeeze Theorem requires practice and familiarity with its applications. Here are some tips to enhance your understanding:

1. Practice with diverse examples: Solve various problems that require applying the Squeeze Theorem to strengthen your skills.
2. Study graphical representations: Visualize functions and their limits to better grasp the concept of squeezing.
3. Collaborate with peers: Discussing problems with classmates can provide new perspectives and insights.

What Are the Limitations of the Squeeze Theorem?

While the Squeeze Theorem is a robust method for evaluating limits, it does have limitations. Some key points to consider include:

• It cannot be used for functions that do not have two bounding functions converging to the same limit.
• The theorem is primarily applicable to limits approaching a specific point, making it less useful for limits at infinity.
• It may not provide insight into the behavior of the function beyond the specific limit being evaluated.

Conclusion: Embracing the Power of the Squeeze Theorem

The Squeeze Theorem is an essential concept in calculus that empowers us to evaluate complex limits with confidence. By understanding its principles, applications, and limitations, we can harness its power to tackle challenging mathematical problems. Whether you are a student, educator, or mathematics enthusiast, the Squeeze Theorem serves as a reminder of the elegance and utility of mathematical reasoning. As we continue to explore the vast landscape of calculus, let us embrace the Squeeze Theorem and use it as a tool for unlocking the mysteries of limits.